2024河南公务员考试每日一练解析(7月30日)

　　1.(单选题)下图是由三个边长分别为4、6、x的正方形所组成的图形，直线AB将它分成面积相等的两部分，则x的值是：

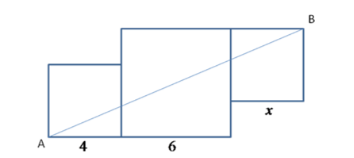
　　A. 3或5

　　B. 2或4

　　C. 1或3

　　D. 1或6

　　解析第一步，本题考查几何问题，属于平面几何类。

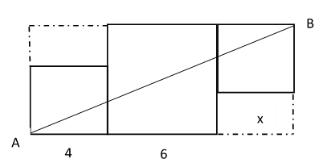
　　第二步，如图所示，将图形补成长方形，AB为对角线，则被AB分开的长方形两部分面积相等。由于原图形中被AB分成的两个部分面积也相等，可推出两个虚线所示的小长方形面积也相等。

　　第三步，4×(6-4)=x×(6-x)，解得x=2或4。

　　因此，选择B选项。

　　2.(单选题)一个圆形，半径变为原来的4倍之后的圆的面积，等于半径增加2厘米之后的面积的4倍，则原来的半径是：

　　A. 1厘米

　　B. 4厘米

　　C. 3厘米

　　D. 2厘米

　　解析第一步，本题考查几何问题，属于平面几何类。

　　第二步，设原来半径为r，半径变为原来的4倍，即为4r，面积为;半径增加2cm后，半径为r+2，面积为。根据题目中的条件可知：，解得r=2。

　　因此，选择D选项。

　　3.(单选题)若将一个长为8厘米、宽为6厘米的长方形盖在一个圆上，两个图形重叠部分的面积占圆的三分之二，占长方形面积的一半。则这个圆的面积为多少平方厘米?

　　A. 64

　　B. 24

　　C. 48

　　D. 36

　　解析第一步，本题考查几何问题，属于平面几何类。

　　第二步，长方形的面积为8×6=48(平方厘米)，重叠面积为48×1/2=24(平方厘米)。由占圆的三分之二，可知圆的面积为24÷2/3=36(平方厘米)。

　　因此，选择D选项。

　　4.(单选题)一个长方体木块恰好能切割成三个正方体木块，三个正方体木块表面积之和比原来的长方体木块的表面积增加了64平方厘米。则长方体木块的体积为()立方厘米。

　　A. 128

　　B. 192

　　C. 256

　　D. 512

　　解析第一步，本题考查几何问题，属于立体几何类。

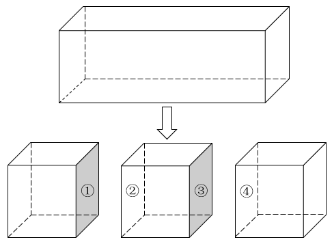
　　第二步，一个长方体锯成三个正方体，如下图：切割之后增加的表面积为4个正方形(①②③④)，每个正方形面积为64/4=16(平方厘米)，可知正方体棱长为4厘米，

　　第三步，长方体的长、宽、高分别为12厘米、4厘米、4厘米，体积为12×4×4=192(立方厘米)。

　　因此，选择B选项。

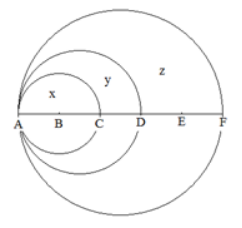
　　5.(单选题)下图为以AC、AD和AF为直径画成的三个圆形，已知AB、BC、CD、DE和EF之间的距离彼此相等。问小圆x、弯月y以及弯月z三部分的面积之比为：

　　A. 4：5：16

　　B. 4：5：14

　　C. 4：7：12

　　D. 4：3：10

　　解析第一步，本题考查几何问题，属于平面几何类。

　　第二步，赋值AB=2，由AB、BC、CD、DE、EF之间的距离相等，可得AC=4、AD=6、AF=10。则小圆、中圆、大圆的半径分别为2、3、5。

　　第三步，小圆x、弯月y以及弯月z的面积分别为4π、9π-4π=5π、25π-9π=16π，故三部分的面积之比为4∶5∶16。

　　因此，选择A选项。

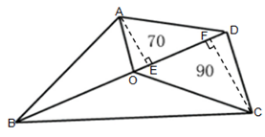
　　6.(单选题)如图所示，公园有一块四边形的草坪，由四块三角形的小草坪组成。已知四边形草坪的面积为480平方米，其中两个小三角形草坪的面积分别为70平方米和90平方米，则四块三角形小草坪中最大的一块面积为多少平方米?

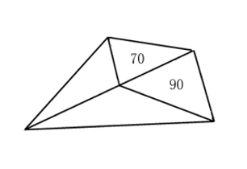
　　A. 120

　　B. 150

　　C. 180

　　D. 210

　　解析第一步，本题考查几何问题，属于平面几何类。

　　第二步，如图所示，△AOD与△COD底边相同(OD)，则面积之比等于高之比，即。同理，△AOB与△COB面积之比等于高之比，即，两三角形面积之和为480-70-90=320(平方米)，可知△BOC面积最大，为(平方米)。

　　因此，选择C选项。

　　7.(单选题)某地市区有一个长方形广场，其面积为1600平方米。由此可知，这个广场的周长至少有：

　　A. 160米

　　B. 200米

　　C. 240米

　　D. 320米

　　解法一：第一步，本题考查几何问题，属于几何特殊性质类。

　　第二步，设长方形的长为x米，宽为米，则长方形的周长为2(x+)米。

　　第三步，根据均值不等式定理，a+b≥2，ab一定，在a=b时，a+b最小。当x=时，即x=40时，周长最小，最小值为2×(40+)=160(米)。

　　因此，选择A选项。

　　解法二：第一步，本题考查几何问题，属于几何特殊性质类。

　　第二步，根据几何特性，长方形面积一定，越接近于正方形时周长越小，本题可直接为正方形，则正方形边长为=40(米)，周长为4×40=160(米)。

　　因此，选择A选项。

　　拓展

　　均值不等式定理：ab2(ab一定)，在a=b时，a+b取得最小值。

　　8.(单选题)一艘非法渔船作业时发现其正右方有海上执法船，于是沿下图所示方向左转30°后，立即以15节(1节=1海里/小时)的速度逃跑，同时执法船沿某一直线方向匀速追赶，并正好在某一点追上。已知渔船在被追上前逃跑的距离刚好与其发现执法船时与执法船的距离相同，问执法船的速度为多少节?

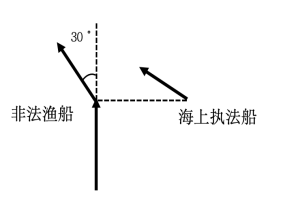
　　A. 20

　　B. 30

　　C.

　　D.

　　第一步，本题考查几何问题，属于平面几何类。

　　第二步，题干中可知∠ABE=30°，则∠ABC=120°，因为渔船逃窜的距离与发现执法船时与执法船的距离相等，即AB=BC。所以∠A=∠C=30°，作BD垂直于AC交AC于D，则AB=2BD，AC=2AD=2BD，所以AC=AB。由于非法渔船和执法船走AB、AC的时间相同，因此速度之比等于距离之比，可知执法船的速度为15海里/小时。

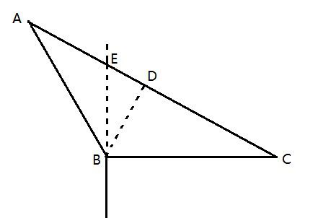
　　因此，选择C选项。

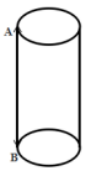
　　9.(单选题)在猫鼠游戏中，跑道为无顶和底的圆柱形，底或顶的圆周长度为5米。圆柱的高为12米，老鼠只能在顶端圆周逃跑并以0.5米/秒的速度从A点出发，与此同时，猫从B点出发匀速追击老鼠，并可以在圆柱形的表面选择任意路线追击。若猫想在A点恰好追击到跑了一圈的老鼠，则它至少要保持的速度为：

　　A. 1.1米/秒

　　B. 1.4米/秒

　　C. 1.3米/秒

　　D. 1.2米/秒

　　解析

　　第一步，本题考查几何问题，属于立体几何类。

　　第二步，圆周长为5米，老鼠以0.5米/秒的速度在顶端圆周逃跑，老鼠跑一圈的时间为(秒)。

　　第三步，猫想在A点恰好追击到跑了一圈的老鼠，时间一定，要想速度尽量慢，则路程最短，即猫跑过的距离恰为圆柱体的高12米。则猫的速度为(米/秒)。

　　因此，选择D选项。

　　10.(单选题)某村民要在屋顶建造一个长方体无盖贮水池，如果池底每平方米的造价为150元，池壁每平方米的造价为120元，那么要造一个深为3米容积为48立方米的无盖贮水池最低造价是多少元?

　　A. 6460

　　B. 7200

　　C. 8160

　　D. 9600

　　解法一：第一步，本题考查几何问题，属于立体几何类，用方程法解题。

　　第二步，总体积为48立方米，深度是3米，那么池底的面积为48÷3=16(平方米)，池底的造价=单价×面积=150×16=2400(元)。

　　第三步，池底的面积为16平方米，设一条底边长为x，则另一条底边长为，池底的周长为，池壁的造价=周长×高×单价，根据均值不等式易知当时总价最低，即x=4(米)，此时池壁的造价为(元)。

　　第四步，总价=池底造价+池壁造价=2400+5760=8160(元)。

　　因此，选择C选项。

　　解法二：第一步，本题考查几何问题，属于立体几何类。

　　第二步，总容积即总体积为48，则底面积为48÷3=16(平方米)。池底造价一定，总价最低则池壁面积最小。池壁面积=底面周长×深度，由几何性质可知当底面是正方形时池底周长最小，此时池底边长为4米，周长为16米，池壁面积=16×3=48(平方米)，池壁造价为48×120=5760(元)，池底造价为16×150=2400(元)，总价为5760+2400=8160(元)。

　　因此，选择C选项。

　　——推荐阅读——

　　【省考快讯】河南省考招录资讯汇总 【备考图书|网课推荐】

　　【历年公告】【历年分数线】【成绩查询】【面试名单查询】【晒分数查分差】

　　【历年招考日程】【招考信息汇总】【点击加微信】【常见问题咨询】

本文标签： （编辑：孙小图）